Answer:
Step-by-step explanation:
Given that:
f = 250 Hz
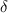 = 2%
= 2%
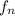 = 600 Hz
= 600 Hz
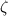 = 0.5 to 1.5 increment by 0.05
= 0.5 to 1.5 increment by 0.05
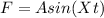
For 250 Hz = 250 cycle/sec
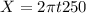
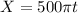
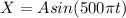
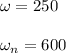
M = 0.98 , 1.02
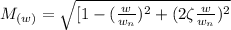
![(1)/(M) = [1-((w)/(w_n))^2]+(2 \zeta (w)/(w_n))^2](https://img.qammunity.org/2021/formulas/engineering/college/xhz5b1ikvwod12n9w2px4sl71trotn90h5.png)
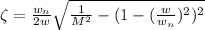
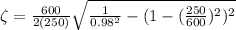

At 0.7183 value of damping ratio the error value was 2% at 0.98 value of M
![(1)/(M) = [1-((w)/(w_n))^2]+(2 \zeta (w)/(w_n))^2](https://img.qammunity.org/2021/formulas/engineering/college/xhz5b1ikvwod12n9w2px4sl71trotn90h5.png)
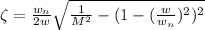
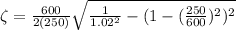
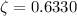
At 0.6330 value of damping ratio the error value was 2% at 1.02 value of M.
Hence, the damping ratio
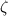 of the transducer must be placed between 0.6330 to 0.7183
of the transducer must be placed between 0.6330 to 0.7183