Question

what is the y-intercept of the line perpendicular to the line y=-3/4x+5 that includes the point (-3,-3)?​

Answer 1

1

Explanation:

For this question, your friend is the point-slope form.

Point-slope form =
`y-y_1 = m(x-x_1)`

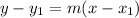
The only variables you replace are m = slope, y1 = y of a given point, and x1 = x of a given point.

First, we need to find the slope that is perpendicular to the equation
`y=-(3)/(4)x+5`

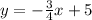
An equation that is perpendicular to another equation have to be negative reciprocals (negative inverse) of each other.

If the slope is 3, then the negative reciprocal of 3 is
`-(1)/(3)`.

So, since the given slope is -3/4, the negative reciprocal is
`(4)/(3)`.

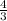We will use the negative reciprocal as m since we are trying to find the equation of line that includes (-3, -3) and is perpendicular to the other equation.

We will use point slope form using the (-3, -3) points and negative reciprocal as m.

`y-y_1 = m(x-x_1)\\y-(-3) = (4)/(3) (x-(-3))\\y+3=(4)/(3)(x+3)`

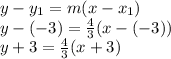
Now, we need to convert this into slope-intercept form. The reason why we need to do this is because y = mx + b, where b is the y-intercept. To do this, solve for y - or in other words, isolate y..

`y+3=(4)/(3)(x+3)\\y+3=(4x)/(3)+4\\y+3-3=(4x)/(3)+4-3\\y=(4)/(3)x+1`

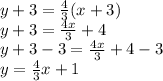
The y-intercept of the line is 1.