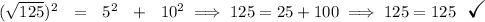Question

The vertices of PQR are P(6, 1), Q(3,5), and R(11, 11). The length of segment PR is √125 units. Use the coordinates and geometric reasoning to show that PQR is a right triangle.Explain your reasoning and show your work​

Answer 1

Check the picture below, so hmm we know that much, and we can also more or less see that PR is the longest side, let's check the length of the other two sides

`~~~~~~~~~~~~\textit{distance between 2 points} \\\\ P(\stackrel{x_1}{6}~,~\stackrel{y_1}{1})\qquad Q(\stackrel{x_2}{3}~,~\stackrel{y_2}{5})\qquad \qquad d = √(( x_2- x_1)^2 + ( y_2- y_1)^2) \\\\\\ PQ=√([3 - 6]^2 + [5 - 1]^2)\implies PQ=√((-3)^2+4^2)\implies \boxed{PQ=5} \\\\[-0.35em] ~\dotfill\\\\ Q(\stackrel{x_1}{3}~,~\stackrel{y_1}{5})\qquad R(\stackrel{x_2}{11}~,~\stackrel{y_2}{11})~\hfill QR=√([11 - 3]^2 + [11 - 5]^2) \\\\\\ QR=√(8^2+6^2)\implies \boxed{QR=10}`

if that's true, the triangle is indeed a right-triangle, then hmmmm most likely using the pythagorean theorem PR² = PQ² + QR², let's check

`(√(125))^2~~ = ~~5^2~~ + ~~10^2\implies 125=25+100\implies 125=125~~\textit{\Large \checkmark}`