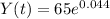Question

Toxic Pollution: In the first year of a study, health officials discovered toxic pollutants in the soil surrounding a factory. The initial measurement was 65 parts per million (ppm) of pollutant. They returned to take similar measurements for several years afterward, and uncovered a disturbing trend. The pollutant levels in the soil surrounding the factory were growing exponentially, at a rate of 4.5% each year. Which exponential model predicts the amount of pollutant in the soil t years from the first measurement?

Answer 1

The model for the pollutant levels in the soil t years from the first measurement is:

`Y(t)=65e^(0.044)`

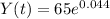
Explanation:

We have a first measurement of 65 parts per million (ppm) of pollutant.

We also know that the pollutant levels were growing exponentially at a rate of 4.5% a year.

We can model this as:

`Y(t)=Y_0e^(kt)`

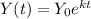
The value of Y0 is the first measurement, that correspond to t=0.

`Y_0=65`

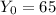
The ratio for the pollutant levels for two consecutive years is 1+0.045=1.045. This can be expressed as the division between Y(t+1) and Y(t), and gives us this equation:

`(Y(t+1))/(Y(t))=(Y_0e^(k(t+1)))/(Y_0e^(kt)) =(e^(k(t+1)))/(e^(kt))=e^(k(t+1-t))=e^k=1.045\\\\\\k=ln(1.045)\approx 0.044`

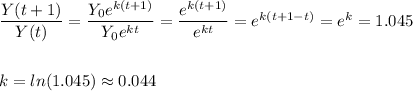
Then, we have the model for the pollutant levels in the soil t years from the first measurement:

`Y(t)=65e^(0.044)`