Question

At which root does the graph of f(x) = (x+4)6(x + 7)5 cross the x axis?

Answer 1

x = -7

Explanation:

f(x) = (x+4)⁶(x + 7)⁵

The roots are when f(x) = 0

(x+4)⁶ = 0

x = -4 (multiplicity 6)

(x+7)⁵ = 0

x = -7 (multiplicity 5)

The graph is tangential to the x-axis on roots with even multiplicity, crosses tge x-axis at roots with odd multiplicity

This graph cuts/crosses the x-axis at x = -7

Answer 2

x = -7

Explanation:

Our function is
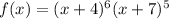`f(x) =(x+4)^6(x+7)^5`. Notice that our possible roots are when x + 4 = 0 and when x + 7 = 0. So, our roots are -4 and -7.

However, the power above x + 4 is even, meaning the graph will simply touch the x-axis at x = -4, but not pass through. The power above x + 7, though, is odd, which means the graph will cross the x-axis.

Thus, the answer is x = -7.