Answer:
A) ∠D ≅ ∠F
Explanation:
Supplementary angles : A pair of angles whose sum is 180° are called supplementary angles
We are given that ∠D is a supplementary angle of ∠E
So,
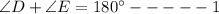
We are also given that ∠F is a supplementary angle of ∠E
So,
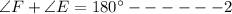
Find the value of ∠E form 1 and 2
From 1 :
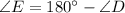
From 2 :
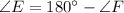
So,

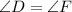
So, Option A is true
Hence ∠D ≅ ∠F