Question

Find the distance between A(3, 2) and B(8,2) a. 2 units b. √5 units c. 3 units d. 5 units​

Answer 1

• 
  `\boxed{\sf{5 \quad units}}`

Explanation:

Use the slope formula.

`\Longrightarrow: \sf{(y_2-y_1)/(x_2-x_1) }`

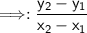
Use the distance formula.

`: \Longrightarrow \sf{√(\left(X_2-X_1\right)^2+\left(Y_2-Y_1\right)^2)}`

`\sf{x_2=8}\\\\\\\sf{x_1=3}\\\\\\\sf{y_2=2}\\\\\\\sf{y_1=2}`

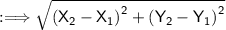
Rewrite the problem down.

`\sf{√(\left(8-3\right)^2+\left(2-2\right)^2)}`

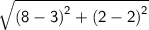
Solve.

Use the order of operations.

PEMDAS stands for:

• Parentheses
• Exponents
• Multiply
• Divide
• Add
• Subtract

⇒ (8-3)²+(2-2)²

Solve parentheses, first.

⇒ (8-3)²

⇒ 8-3=5

⇒ 5²+(2-2)²

⇒ (2-2)=0

⇒ 0²

Rewrite the problem down.

⇒ 5²+0²

Do exponents next.

⇒ 5²=5*5=25

⇒ 0²=0*0=0

⇒ 25+0

Add.

⇒ 25+0=25

You can also divide the numbers from left to right.

→ 25/5=5

• Therefore, the distance between (3, 2) and (8,2) is "5 units", which is our answer.

I hope this helps. Let me know if you have any questions.