Question

A. When light of wavelength 250 nm is incident on a metal surface, the maximum speed of the photoelectrons is 4.0 × 105 m/s, what is the work function of the metal in electron volts? [10 marks] B. Assume that a 100-W light bulb gives off 2.50% of its energy as visible light of wavelength 500 nm. How many photons of visible light are given off in 1.0 min? Page 7 of 7 C. A small blood vessel near the skin surface has a radius of 10 μm, a length of 1 μm and the pressure drop along the blood vessel is 2.50 Pa. The viscosity of blood is 0.0027 Pa.s. i. What is the volume flow rate of blood through this blood vessel? What is the velocity of blood flow? [6 marks] ii. Vasodilation causes the radius of this blood vessel to increase to 12 μm, while leaving the pressure drop along the vessel unchanged? What is the volume flow rate through this blood vessel now? What is the velocity of blood flow? D. Many radioisotopes have important industrial, medical, and research applications. One of these is Cobalt-60, which has a half-life of 5.20 years and decays by the emission of a beta particle (energy 0.31 MeV) and two gamma photons (energies 1.17 MeV and 1.33 MeV). A scientist wishes to prepare a Cobalt-60 sealed source that will have an activity of at least 10 Ci after 30 months of use. i. What minimum initial mass of Cobalt-60 is required? [6 marks] ii. At what rate will the source emit energy after 30 months? [4 marks] E. The radioactive isotope Gold-198 has a half-life of 64.80 hrs. A sample containing this isotope has an initial activity of 40.0 μCi. Calculate the number of nuclei that will decay in the time interval from 10 hrs to 12 hrs. [10 marks]

Answer 1

Step-by-step explanation:

Part A

- Work function ( ∅ ) is the minimum energy required by the photon to knock an electron out of the metal surface. That is the portion of energy of a photon transferred to an electron so that it can escape the metal.

- We can mathematically express it:

∅ = Ep - Ek

=
`(h*c)/(lamba) - 0.5*m_e*v^2_e\\`

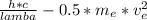
Where,

Planck's constant ( h ) = 6.6261*10^-34

Speed of light ( c ) = 3*10^8 m/s

mass of an electron ( m_e ) = 9.1094*10^-31 kg

Given:-

Incident light's wavelength ( λ ) = 250*10^-9 m

The maximum speed o electron ( v_e ) = 4*10^5 m/s

Solution:-

- Plug the values into the expression derived before:

∅ =
`((6.6261*10^-^3^4)*(3*10^8))/(250*10^-^9) \\\\`

∅ =
`7.22257*10^-^1^9 J * (6.242*10^1^8 eV)/(J)`

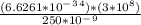
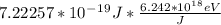
∅ = 4.508 eV ... Answer

Part B

- 2.5% of the energy emitted by a 100-W light bulb was visible light with wavelength ( λ ) = 500*10^-9 m. In 1.0 min the amount of energy harbored by a stream of photons are:

`E_p = n_p*(h*c)/(lambda) = P*t*e`

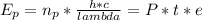
Where,

Planck's constant ( h ) = 6.6261*10^-34

Speed of light ( c ) = 3*10^8 m/s

Given:-

visible light's wavelength ( λ ) = 500*10^-9 m

Power of light bulb ( P ) = 100 W

Time taken ( t ) = 1.0 min = 60 s

Portion of energy as light ( e ) = 0.025

Solution:-

- Plug the values into the expression derived before:

`n_p = ((lambda)*(P)*(t)*(e))/(h*c) \\\\n_p = ((500*10^-^9)*(100)*(60)*(0.025))/((6.6261*10^-^3^4)*(3*10^8)) \\`

n_p = 3.773 * 10^20 ... Answer

Part C

- A blood vessel of radius ( r ) with length ( L ) carries blood with viscosity ( μ ). The pressure drop ( ΔP ) in the blood vessel was witnessed.

- Pressure loss ( ΔP ) in a cylindrical blood vessel is given by the Darcy's equation given below:

`(dP)/(p) = f*(L)/(D)*(v^2)/(2)`

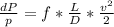
Where,

ρ: Density of blood

f: Friction factor

D: Diameter of vessel

v: Average velocity

- The friction factor is a function of Reynolds number and relative roughness of blood vessel. We will assume the blood vessel to be smooth, round and the flow to be laminar ( later verified ).

- The flow rate ( Q ) in a smooth blood vessel subjected to laminar flow conditions is given by the Poiseuille's Law. The law states:

`Q = (\pi*dP*r^4 )/(8*u*L)`

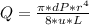
- The velocity ( v ) in a circular tube is given by the following relation:

`v = (Q)/(\pi*r^2 )`

Given:-

dP ( Pressure loss ) = 2.5 Pa

radius of vessel ( r ) = 10μm = 10*10^-6 m

viscosity of blood ( μ ) = 0.0027 Pa.s

Length of vessel ( L ) = 1μm = 10^-6 m

Solution:-

- Use the Poiseuille's Law to determine the flow rate ( Q ) of the blood in the vessel:

`Q = (\pi*(2.5)*(10*10^-^6)^4 )/(8*(0.0027)*(10^-^6))`

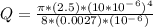
Q = 3.6361*10^-12 m^3 / s

- The corresponding velocity ( v ) of the blood flow would be:

`v = (3.6361*10^-^1^2)/(\pi*(10*10^-^6)^2 )`

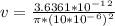
v = 0.01157 m/s

- Use the Poiseuille's Law to determine the flow rate ( Q ) of the blood blood in the enlarged vessel ( r = 12 μm = 10*10^-6 m ) :

`Q = (\pi*(2.5)*(12*10^-^6)^4 )/(8*(0.0027)*(10^-^6))`

Q = 7.54*10^-12 m^3 / s

- The corresponding velocity ( v ) of the blood flow would be:

`v = (7.53982*10^-^1^2)/(\pi*(12*10^-^6)^2 )`

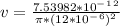
v = 0.01666 m/s

Part D

- A radioactive isotope of Cobalt ( Co - 60 ) undegoes Beta decay ( 0.31 MeV ) and emits two gamma rays of energy ( 1.17 & 1.33 ) MeV.

- The radioactive decay for the ( Cobalt - 60 ) can be expressed in form of an equation:

`_2_7Co ( 60 ) ---> _2_8 Ni ( 60 ) + e^- + v_e^- + gamma`

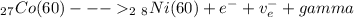
- The half life ( T_1/2 ) of the Co-60 can be used to determine the decay constant ( λ ):

λ =
`lambda = (Ln(2))/(T_1/2)\\`

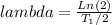
Where,

T_1/2 = 5.2 yrs = 1.68*10^8 s

Hence, the decay constant is

λ =
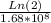`(Ln ( 2 ) )/(1.68*10^8)` = 4.22*10^-9 s^-1

- The activity ( A ) of any radioactive isotope is function of time ( t ) defined by negative exponential distribution:

`A = A_o*e^(^-^l^a^m^b^d^a^*^t^)`

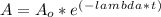
Where,

A_o: The initial activity ( Bq )

- The activity of the radioactive isotope Co-60 was A = 10 Ci after t = 30 months. The initial activity ( A_o ) can be determined:

`A_o= (A)/(e^(^-^l^a^m^b^d^a^*^t^)) \\\\A_o= ((10Ci)*(3.7*10^1^0 Bq/Ci))/(e^(^-^4^.^2^2^*^1^0^-^9*^7^.^8^8^*^1^0^7^)) \\`

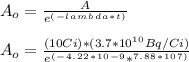
A_o = 5.016 * 10^11 Bq

- The initial number of nuclei in the sample ( N_o ) is given by:

`N_o = (A_o) / (lambda)\\\\N_o = (5.016*10^1^1)/(4.22*10^-^9) = 1.22*10^2^2`

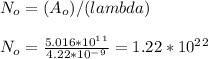
- The initial mass of Co-60 used as a sample can be determined:

`m_o = M_r*N_o\\\\m_o = (59.933822u)*(1.66*10^-^2^7)*(1.22*10^2^2)\\`

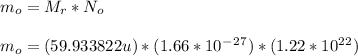
m_o = 12.2 * 10^-6 kg ... Answer

- The total energy ( E ) released from the beta decay transformation:

E = E(β) + E(γ1) + E(γ2) = 0.31 + 1.17 + 1.33 = 2.81 MeV

- The rate at which the source emits energy after 30 months:

P = E*A =
`( 2.81 MeV * (1.6*10^-^1^3 J)/(MeV) ) * ( 10 Ci * (3.7*10^1^0 Bq)/(Ci) )`

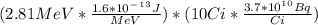
P = 0.166 W .. Answer