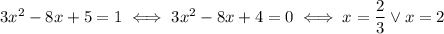Question

Solve x :

`{(3 {x}^(2) - 8x + 5)}^(x + 1) = 1`
​

Answer 1

x = -1, ⅔, 2

Explanation:

3x² - 8x + 5

3x² - 3x - 5x + 5

3x(x - 1) - 5(x - 1)

(3x - 5)(x - 1)

[3x² - 8x + 5]^(x+1) = 1

The ourput is 1 when:

1) The power is 0

x + 1 = 0

x = -1

2) base is 1

3x² - 8x + 5 = 1

3x² - 8x + 4 = 0

3x² - 6x - 2x + 4 = 0

3x(x - 2) - 2(x - 2) = 0

(3x - 2)(x - 2) = 0

x = 2 , ⅔

Therefore, 3 solutions

x = -1, ⅔ , 2

Answer 2

We want this expression to fall in one of the two cases:

`\alpha ^ 0 = 1 = 1^\beta`

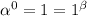
So, if the exponent is zero, the base can assume any value, because everything (expect zero) to the power of zero is one.

Similarly, if the base is 1, the exponent can be any number, becuase 1 raised to any exponent is still one.

If we are looking for the "zero exponent" strategy, we simply have to impose

`x+1=0\iff x=-1`

In this case, the expression becomes
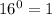`16^0=1`, so we avoided the
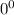`0^0` case and we're good.

If we are looking for the "base equals one" strategy, we must impose

`3x^2-8x+5 = 1 \iff 3x^2-8x+4=0 \iff x=(2)/(3)\lor x=2`