Question

When subject to an unknown torque, the shear stress in a 2 mm thick rectangular tube of dimension 100 mm x 200 mm was found to be 50 MPa. Using the same amount of material, if the dimensions are changed to 50 mm x 250 mm, what will be the shear stress (in MPa)? The breadth and depth of the section are given along the centreline of the wall.

Answer 1

The shear stress will be 80 MPa

Step-by-step explanation:

Here we have;

τ = (T·r)/J

For rectangular tube, we have;

Average shear stress given as follows;

Where;

`\tau_(ave) = (T)/(2tA_(m))`

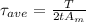
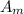`A_m` = 100 mm × 200 mm = 20000 mm² = 0.02 m²

t = Thickness of the shaft in question = 2 mm = 0.002 m

T = Applied torque

Therefore, 50 MPa = T/(2×0.002×0.02)

T = 50 MPa × 0.00008 m³ = 4000 N·m

Where the dimension is 50 mm × 250 mm, which is 0.05 m × 0.25 m

Therefore,
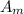`A_m` = 0.05 m × 0.25 m = 0.0125 m².

Therefore, from the following average shear stress formula, we have;

`\tau_(ave) = (T)/(2tA_(m))`

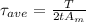
Plugging in then values, gives;

`\tau_(ave) = (4000)/(2* 0.002 * 0.0125) = 80,000,000 Pa`

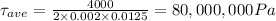
The shear stress will be 80,000,000 Pa or 80 MPa.