Question

James has a desk job and would like to become more fit, so he purchases a tread walker and a standing desk which will allow him to walk at a slow pace as he works. However, he is concerned that standing and walking while working may cause his productivity to decline. After working this way for 6 months he takes a simple random sample of 15 days. He records how long he walked that day (in hours) as recorded by his fitness watch as well as his billable hours for that day as recorded by a work app on his computer. Assuming that all conditions for inference are met, which of the following is a 95 percent confidence interval for the average change in the number of billable hours for each increase of 1 hour spent walking?

Answer 1

The correct answer is C. [-0.245±2.160*0.205]

Explanation:

Hello!

To analyze the if walking while working (independent variable X) affects his working productivity (dependent variable Y) James took a random sample of 15 days (from a 6 month period in which he worked and trained at home) and recorded how long he walked and his billable hours for that day.

Using this information he estimated the linear regression between the working productivity and the time spent training.

^Y= 7.785 -0.245X

The interest is to estimate the change in the average number of billable hours every time he increases the time spent walking in 1 hour.

To estimate the range of values the average billable hours may take each time the training time increases sone hour, you have to calculate a confidence interval for the population slope of the regression. The statistic is a t-test:

`t= (b-\beta)/(Sb) ~~t_(n-1)`

[b±
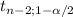`t_(n-2;1-\alpha /2)`*Sb]

Using a 95% confidence level the value of t is
`t_(n-2;1-\alpha /2)= t_(13; 0.975)= 2.160`

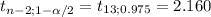
b= -0.245

Sb= 0.205

[-0.245±2.160*0.205]

[-0.68780.1978]

Using a 95% confidence level you'd expect the interval [-0.68780.1978] to contain the value of the average billable hours when the time spent walking increases in 1 hour.

I hope this helps!

Answer 2

answer is

`-0.245 \pm2.160(0.205)`

Explanation:

After working this way for 6 months he takes a simple random sample of 15 days. He records how long he walked that day (in hours) as recorded by his fitness watch as well as his billable hours for that day as recorded by a work app on his computer.

Slope is -0.245

Sample size n = 15

Standard error is 0.205

Confidence level 95

Sognificance level is (100 - 95)% = 0.05

Degree of freedom is n -2 = 15 -2 = 13

Critical Value =2.16 = [using excel = TINV (0.05, 13)]

Marginal Error = Critical Value * standard error

= 2.16 * 0.205

= 0.4428

`-0.245 \pm2.160(0.205)`