Answer:
The product of the complex numbers is 6cis55°
Explanation:
Given the complex numbers in polar cordinates
[2cis 33˚][3cis 22˚]
Generally, if z = rcis
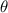 , then z = r(cos
, then z = r(cos
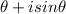 )
)
2cis33° = 2(cos33°+isin33°)
3cis22° = 3(cos22°+isin22°)
Taking tthe product of both complex numbers;
[2cis 33˚][3cis 22˚] = [2(cos33°+isin33°)][3(cos22°+isin22°)]
= 6{cos33cos22+icos33sin22+isin33cos22+i²sin33sin22}
since i² = 1
= 6{cos33cos22+icos33sin22+isin33cos22-sin33sin22}
= 6{(cos33cos22-sin33sin22)+i(cos33sin22+sin33cos22)}
Applying the trigonometric identity as shown;
cos(A+B)= cosAcosB-sinAsinB and;
sin(A+B)= sinAcosB + cosAsinB
[2cis 33˚][3cis 22˚] = 6{(cos(33+22)+ i(sin(33+22)}
[2cis 33˚][3cis 22˚] = 6(cos55°+isin55°)
[2cis 33˚][3cis 22˚] = 6cis55°
The product of the complex numbers is 6cis55°