Answer:
The total volume of the prism is 32.49 cubic centimeters.
The total surface area of the figure is 111.66 square centimeters.
Explanation:
This problem is about finding the volume of a prism which base is an equilateral triangle.
The volume of the prism would be defined as
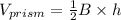
Where
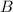 is the area of the base and
is the area of the base and
 is the height of the prism.
is the height of the prism.
The area of the equilateral triangle at the base is
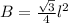
Where
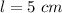
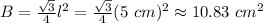
Replacing the base area in the volume formula, we have
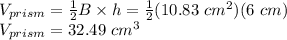
Therefore, the total volume of the prism is 32.49 cubic centimeters.
Now, the total surface area would be the sum of three rectangle faces and two triangles faces.
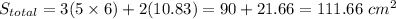
Therefore, the total surface area of the figure is 111.66 square centimeters.