Question

Problem 1.) A researcher claims that 96% of college graduates say their college degree has

been a good investment. In a random sample of 2000 graduates, 1500 say their college degree has
been a good investment. At a = 0.05 is there enough evidence to reject the researcher's claim?

Answer 1

|Z| = |-52.5| = 52.5 > 1.96 at 0.05 level of significance

Null hypothesis is rejected

We rejected the researcher's claim

A researcher do not claims that 96% of college graduates say their college degree has been a good investment.

Explanation:

Explanation:-

Given data A researcher claims that 96% of college graduates say their college degree has been a good investment.

Population proportion 'P' = 0.96

Q = 1-P = 1- 0.96 = 0.04

In a random sample of 2000 graduates, 1500 say their college degree has

been a good investment.

Sample proportion

`p^(-) = (x)/(n) = (1500)/(2000) = 0.75`

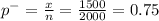
Level of significance ∝ = 0.05

`Z_{(\alpha )/(2) } = Z_{(0.05)/(2) } = Z_(0.025) = 1.96`

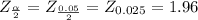
Test statistic

`Z = \frac{p^(-) - P }{\sqrt{(PQ)/(n) } }`

`Z = \frac{0.75 - 0.96 }{\sqrt{(0.96 X 0.04)/(2000) } }`

`Z = (-0.21)/(0.00435) = -52.5`

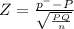
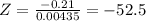
|Z| = |-52.5| = 52.5 > 1.96 at 0.05 level of significance

Null hypothesis is rejected

We rejected the researcher's claim

Conclusion:-

A researcher do not claims that 96% of college graduates say their college degree has been a good investment.