Question

A rectangular playground is 10m longer than it is wide.The area of the playground is 1400m² Calculate the width and length of the playground. solve using quadratic formula please?

Answer 1

Explanation:

Given Data:

Area = 1400m²

L = 4+w

W= w

Area = L * W

1400 = ( 4+W) W ²

1400 = 4w + w ²

w ² + 4w - 1400 = 0

- b ± √ b ² - 4ac / 2a

Where;

a = 1

b = 4

c = -1400

- 4 ± √4² - 4(1)(-1400) / 2(1)

= - 4 ± 74.94 /2

= - 4 + 74.94 / 2 or - 4 - 74.94 / 2

= 35.47 or - 39.47

Answer 2

`1400 = x(x+10)= x^2 +10x`

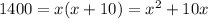
We can rewrite this expression like this:

`x^2 +10 x -1400 =0`

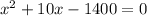
And we can use the quadratic formula given by:

`x = (-b \pm √(b^2 -4ac))/(2a)`

Where
`a =1 , b=10 , c= -1400`

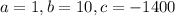
And replacing we got:

`x = (-10 \pm √(10^2 -4(10)(-1400)))/(2*1)`

And solving we got:

`x_1 =32.75 , x_2 = -42.75`

And since the value can't be negative the answer would be x = 32.75 and the value of y = 32.75+10 =42.75

Explanation:

For this case we know that we have a rectangular playground and the area can be founded with this formula:

`A = xy`

Where x represent the width and y the length. From the problem we know that A =1400 m^2 and the heigth is 10m longer than the wide so we can write this condition as:

`y = 10 +x`

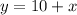
And replacing this formula into the area we got:

`1400 = x(x+10)= x^2 +10x`

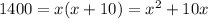
We can rewrite this expression like this:

`x^2 +10 x -1400 =0`

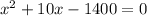
And we can use the quadratic formula given by:

`x = (-b \pm √(b^2 -4ac))/(2a)`

Where
`a =1 , b=10 , c= -1400`

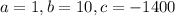
And replacing we got:

`x = (-10 \pm √(10^2 -4(10)(-1400)))/(2*1)`

And solving we got:

`x_1 =32.75 , x_2 = -42.75`

And since the value can't be negative the answer would be x = 32.75 and the value of y = 32.75+10 =42.75