Question

On the spinner, the probability of landing on black is 1/2 , and the probability of landing on red is 1/3. Create a probability distribution for the experiment of spinning the spinner.

Answer 1

1/27

Explanation:

Answer 2

1)
`p_i \geq 0 , \forall i`

2)
`\sum_(i=1)^n P_i = 1, i =1,2,...,n`

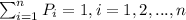
And for this case we have:

`(1)/(2)+(1)/(6)= (2)/(3)`

By the complement rule we can find the probability that the spinner land in a non black or red space:

`p(N) = 1- (1)/(2) -(1)/(3)= (1)/(6)`

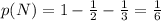
And then the probability distribution would be:

Color Red Black N

Prob. 1/3 1/2 1/6

Explanation:

For this case we have two possible outcomes for the spinner experiment:

`p(black) =(1)/(2)`

`p(red) = (1)/(3)`

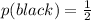
In order to have a probability distribution we need to satisfy two conditions:

1)
`p_i \geq 0 , \forall i`

2)
`\sum_(i=1)^n P_i = 1, i =1,2,...,n`

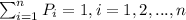
And for this case we have:

`(1)/(2)+(1)/(6)= (2)/(3)`

By the complement rule we can find the probability that the spinner land in a non black or red space:

`p(N) = 1- (1)/(2) -(1)/(3)= (1)/(6)`

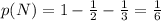
And then the probability distribution would be:

Color Red Black N

Prob. 1/3 1/2 1/6