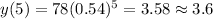Answer:
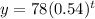
And for this case we want to identify the initial amount and for this case would be 78. And the growth rate can be obtained from the term inside of the parenthesis.
The general model is given by this model:
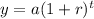
And then
 and
and

And then we want to find the of the function at t=5 and we got:
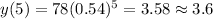
Explanation:
For this case we have the following function given:
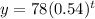
And for this case we want to identify the initial amount and for this case would be 78. And the growth rate can be obtained from the term inside of the parenthesis.
The general model is given by this model:
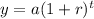
And then
 and
and

And then we want to find the of the function at t=5 and we got: