Question

A new kind of rocket takes off along an exponential trajectory, with height, in miles, represented by 3x, where x is the time, in seconds. Find the time when the height of the rocket is 8 miles.

What is the exact solution written as a logarithm?

What is an approximate solution rounded to the nearest thousandth?

Answer 1

We have been given that a new kind of rocket takes off along an exponential trajectory, with height, in miles, represented by
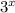`3^x`, where x is the time, in seconds. We are asked to find the time when the height of the rocket id 8 miles.

To find the time, we will equate height function with 8 and solve for x as:

`3^x=8`

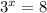
To solve for x, we will take natural log on both sides as:

`\ln(3^x)=\ln (8)`

We can rewrite 8 as
`2^3`.

`\ln(3^x)=\ln (2^3)`

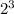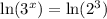
Using natural log property
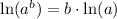`\ln(a^b)=b\cdot \ln(a)`, we will get:

`x\cdot \ln(3)=3\cdot\ln (2)`

`(x\cdot \ln(3))/( \ln(3))=(3\cdot\ln (2))/( \ln(3))`

`x=(3\cdot\ln (2))/( \ln(3))`

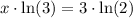
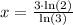
Therefore, exact solution will be
`(3\cdot\ln (2))/( \ln(3))`.

`x=(2.0794415416798359)/(1.0986122886681097)`

`x=1.892789260714`

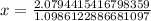
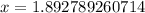
Upon rounding to nearest thousandth, we will get:

`x\approx 1.89`

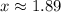
Therefore, the height of the rocket will be 8 miles after approximately 1.89 seconds.