Question

Find the length of side AB
Give answer to 3 significant figures

Answer 1

AB = 8.856 cm
Rounded would get you 8.86 cm.
Hope this helps.

Explanation:

I don't know how I got it but it's right.

Answer 2

AB = 8.857 cm

Explanation:

Here, we are given a right angle
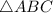`\triangle ABC` in which we have the following things:

`\angle A = 90 ^\circ\\\angle C = 41 ^\circ\\\text{Side }BC = 13.5 cm`

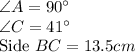
Side BC is the hypotenuse here.

We have to find the side AB.

Trigonometric functions can be helpful to find the value of Side AB here.

Calculating
`\angle B`:

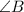Sum of all the angles in
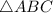`\triangle ABC` is
`180^\circ`.

`\Rightarrow \angle A + \angle B + \angle C = 180^\circ\\\Rightarrow 90^\circ + \angle B + 41^\circ = 180^\circ\\\Rightarrow \angle B = 49^\circ`

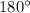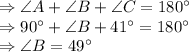
We know that cosine of an angle is:

`cos \theta = \frac{\text{Base}}{\text{Hypotenuse}}\\\Rightarrow cos B = (AB)/(BC)\\\Rightarrow cos 49^\circ = (AB)/(13.5)\\\Rightarrow AB = 13.5 * 0.656\\\Rightarrow AB = 8.857 cm`

So, side AB = 8.857 cm .