Answer:
C. The 6th term is positive/negative 80
Explanation:
Given
Geometric Progression
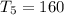
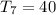
Required
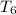
To get the 6th term of the progression, first we need to solve for the first term and the common ratio of the progression;
To solve the common ratio;
Divide the 7th term by the 5th term; This gives
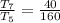
Divide the numerator and the denominator of the fraction by 40
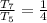 ----- equation 1
----- equation 1
Recall that the formula of a GP is
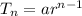
Where n is the nth term
So,
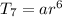
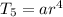
Substitute the above expression in equation 1
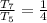 becomes
becomes
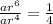

Square root both sides
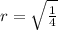
r = ±

Next, is to solve for the first term;
Using
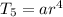
By substituting 160 for T5 and ±
 for r;
for r;
We get

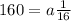
Multiply through by 16
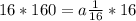
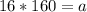
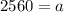
Now, we can easily solve for the 6th term
Recall that the formula of a GP is
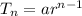
Here, n = 6;
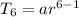
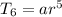
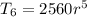
r = ±

So,
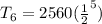 or
or
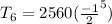
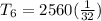 or
or
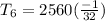
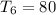 or
or
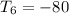
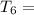 ±80
±80
Hence, the 6th term is positive/negative 80