Question

La profesora de matemáticas solicita a dos estudiantes que describan las cosas que les han parecido interesantes de los números primos y de los números compuestos, a lo que dos estudiantes responden: Paola: he descubierto que cualquier número compuesto par se puede escribir como la multiplicación de factores primos. Edwin: he descubierto que cualquier número compuesto impar se puede escribir como la suma de dos números primos. La profesora pide a los estudiantes que examinen las ideas expuestas por Paola y Edwin y verifiquen si son verdaderas o falsas. De acuerdo con las afirmaciones hechas por Paola y Edwin es CORRECTO afirmar que A. ambas afirmaciones son falsas. B. ambas afirmaciones son verdaderas. C. la afirmación de Paola es falsa y la de Edwin es verdadera. D. la afirmación de Paola es verdadera y la de Edwin es falsa. The math teacher asks two students to describe the things they found interesting about the prime and composite numbers, to which two students respond:

Paola: I have discovered that any even compound number can be written as the multiplication of prime factors.
Edwin: I have discovered that any odd compound number can be written as the sum of two prime numbers.

The teacher asks students to examine the ideas put forth by Paola and Edwin and check to see if they are true or false.

According to the statements made by Paola and Edwin, it is CORRECT to affirm that

TO.
both statements are false.

B.
both statements are true.

C.
Paola's statement is false and Edwin's is true.

D.
Paola's statement is true and Edwin's is false.

Answer 1

Respuesta D

Explanation:

Paola afirma: Todo número compuesto par, se puede escribir como la multiplicación de factores primos.

Esta afirmación es cierta, pues es un caso de la afirmación de que todo número natural mayor que uno se puede escribir como multiplicación de números primos. A este proceso se le llama descomposición en factores primos.

Edwin afirma: Todo número compuesto impar se puede escribir como la suma de dos números primos.

Esta afirmación es falsa. Note que al sumar dos números impares de la forma 2k+1 y 2m+1 para k distinto de m, se obtiene

`2k+1+2m+1 = 2(km+1)`

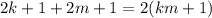
Es decir, la suma de dos números impares es siempre par.

Note que a excepción de 2, todo número primo es impar. Para que esta afirmación fuera cierta, necesariamente tendría que pasar que cualquier número impar k se escriba de la forma p+2 donde p es un número primo. Esto es equivalente que para cualquier número impar k, el número k-2 sea primo.

Basta con dar un ejemplo para ver que esto no pasa. Tomemos k=11. En este caso, k-2 = 9, el cuál no es un número primo. Entonces 11 no se puede descomponer como la suma de dos números primos.