Question

The graph of y = 02 is translated 2 units right and 5 units down. Write an equation for the function in vertex form and in standard form.

vertex form: y
standard form: y =​

Answer 1

An equation for the function in vertex form and in standard form include:

vertex form:
`y = (x - 2)^2 -5`

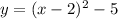
standard form:
`y=x^(2) -4x-1`

In Mathematics and Euclidean Geometry, the vertex form of a quadratic function is represented by the following mathematical equation:

`y = a(x - h)^2 + k`

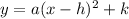
Where:

• h and k represents the vertex of the graph.
• a represents the leading coefficient.

Since the graph of the parent quadratic function was horizontally translated 2 units right and vertically translated 5 units down, the transformed quadratic function can be written in vertex form as follows;

`y = (x - 2)^2 -5`

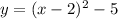
Next, we would rewrite the quadratic function in standard form;

`y = (x - 2)^2 -5\\\\y = x^(2) -2x-2x+4 -5\\\\y=x^(2) -4x-1`

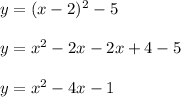
Complete Question:

The graph of
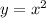`y=x^(2)` is translated 2 units right and 5 units down. Write an equation for the function in vertex form and in standard form.

vertex form: y

standard form: y =​

Answer 2

Vertex: y = (x - 2)² - 5

Standard: y= x² - 4x - 1

Explanation:

If y = x²

After 2 units towards the right,

y = (x - 2)²

After 5 units downwards

y = (x - 2)² - 5

y = x² - 4x + 4 - 5

y = x² - 4x - 1