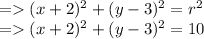Question

Write the equation of circle b with center B(-2,3) that passes through (1,2)

Answer 1

`(x+2)^2 + (y-3)^2 = 10`

Explanation:

The standard equation for circle is

`(x-a)^2 + (y-b)^2 = r^2`

where point (a,b) is coordinate of center of circle and r is the radius.

______________________________________________________

Given

center of circle =((-2,3)

let r be the radius of circle

Plugging in this value of center in standard equation for circle given above we have

`(x-a)^2 + (y-b)^2 = r^2 \ substitute (a,b) \ with (-2,3) \\=>(x-(-2))^2 + (y-3)^2 = r^2 \\=>(x+2)^2 + (y-3)^2 = r^2 (1)`

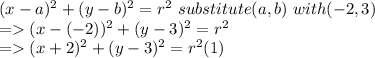
Given that point (1,2 ) passes through circle. Hence this point will satisfy the above equation of circle.

Plugging in the point (1,2 ) in equation 1 we have

`\\=>(x+2)^2 + (y-3)^2 = r^2 \\=> (1+2)^2 + (2-3)^2 = r^2\\=> 3^2 + (-1)^2 = r^2\\=> 9 + 1 = r^2\\=> 10 = r^2\\=> r^2 = 10\\`

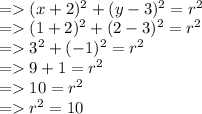
now we have value of r^2 = 10, substituting this in equation 1 we have

Thus complete equation of circle is
`=>(x+2)^2 + (y-3)^2 = r^2\\=>(x+2)^2 + (y-3)^2 = 10`