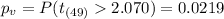Answer:
We want to verify if the mean age of online consumers has decreased (23.3), the system of hypothesis would be:
Null hypothesis:
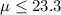
Alternative hypothesis:
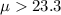
And the correct option would be:
a. H0: μ = 23.3 Ha: μ > 23.3
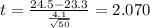
The degrees of freedom are given by:
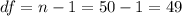
And the p value would be:
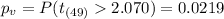
Explanation:
Information provided
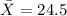 represent the sample mean for the age of online purchases
represent the sample mean for the age of online purchases
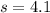 represent the sample standard deviation
represent the sample standard deviation
 sample size
sample size
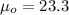 represent the value to verify
represent the value to verify
t would represent the statistic
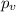 represent the p value
represent the p value
System of hypothesis
We want to verify if the mean age of online consumers has decreased (23.3), the system of hypothesis would be:
Null hypothesis:
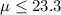
Alternative hypothesis:
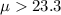
And the correct option would be:
a. H0: μ = 23.3 Ha: μ > 23.3
The statistic is given by:
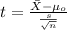 (1)
(1)
Replacing the info we got:
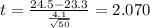
The degrees of freedom are given by:
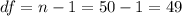
And the p value would be: