Answer:
Check the explanation
Explanation:
We want to estimate the total weight of grain on the field based on the data on a simple random sample of 5 piles out of 200. The population and sample sizes are N=200 & n=5 respectively.
1) Let Y_1,Y_2,...,Y_{200} be the weight of grain in the 200 piles and y_1,y_2,...,y_{5} be the weights of grain in the pile from the simple random sample.
We know, the sample mean is an unbiased estimator of the population mean. Therefore,
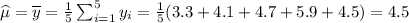
where \mu is the mean weight of grain for all the 200 piles.
Hence, the total grain weight of the population is
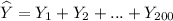
=
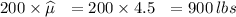
2) To calculate a bound on the error of estimates, we need to find the sample standard deviation.
The sample standard deviation is
S=
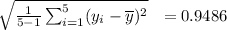
Then, the standard error of

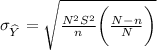 =83.785
=83.785
Hence, a 95% bound on the error of estimates is
![[\pm z_(0.025)* \sigma_{\widehat{Y}}]\: \: \: =[\pm 1.96* 83.875]\: \: \: =[\pm 164.395]](https://img.qammunity.org/2021/formulas/mathematics/college/r6cokk5h16g0aimpncfwl79k6sehbx8ks4.png)
3) Let x_1,x_2,...,x_5 denotes the total weight of the sampled piles.
Mean total weight of the sampled piles is
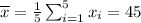
The sample ratio is
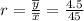 =0.1 , this is also the estimate of the population ratio R=
=0.1 , this is also the estimate of the population ratio R=
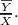
Therefore, the estimated total weight of grain in the population using ratio estimator is
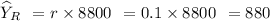 lbs
lbs
4) The variance of the ratio estimator is
var(r)=
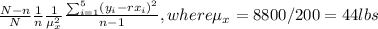
=
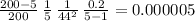
Hence, the standard error of the estimate of the total population is
 =21.556
=21.556
Hence, a 95% bound on the error of estimates is
![[\pm z_(0.025)* \sigma_(R)]\: \: \: =[\pm 1.96* 21.556]\: \: \: =[\pm 42.25]](https://img.qammunity.org/2021/formulas/mathematics/college/fxuib4rlfl8be6pwebrsu8rhaswrohjpsp.png)