The answers are :
m∠C ≈ 27.2°
a (side AC) ≈ 50.4
b (side AB) ≈ 17.5
Given: triangle ABC with ∠CAB = 24°, ∠CBA = 66°, and BC = 43. We need to find ∠C, a (side AC), and b (side AB).
Steps:
1. Solve for m∠C: Use the Law of Sines:
(sin∠C/(BC)) = (sin∠B/(AC))
Substitute known values and solve for ∠C:
sin ∠C = (BC * sin ∠B)/(AC) = (43* sin(66°))/(2AC * sin(24° + 66°))
Using inverse sine (arcsin) function:
∠C ≈
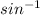 ((43 * sin(66°))/(2AC * sin(90°)))
((43 * sin(66°))/(2AC * sin(90°)))
Note that we used 90° because ∠A + ∠B + ∠C = 180° and we already know ∠A and ∠B.
Calculating with a calculator and rounding to the nearest tenth:
∠C ≈ 27.2°
2. Solve for a (side AC): Use the same Law of Sines equation as in step 1, but solve for AC:
AC = (BC * sin ∠B)/{\sin ∠C}
Substitute known values and solve for AC:
AC = ((43 * sin(66°))/(sin(27.2°)) ≈ 50.4
3. Solve for b (side AB):** Use the Law of Cosines:
b² = a² + c² - 2ac cos(∠C)
Substitute known values and solve for b:
b² = 50.4² + 43² - 2(50.4)(43) cos(27.2°)
Taking the square root of both sides:
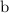 ≈
≈
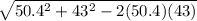 cos(27.2°) ≈ 17.5
cos(27.2°) ≈ 17.5
m∠C ≈ 27.2°
a (side AC) ≈ 50.4
b (side AB) ≈ 17.5