Answer:
a.
radius = 9.8551 cm
height = 9.8551 cm
b.
area = 915.3633 cm^2
Explanation:
a.
Let the radius of the cylinder be r, and let the height of the cylinder be h.
Volume of the cylinder:


Solve for h:
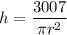
Surface area of the cylinder (lateral are + 1 base only):

Substitute h found above:
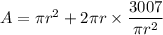
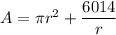
Take the first derivative of the area with respect to the radius.


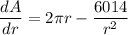
Set the derivative equal to zero and solve for r.
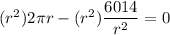
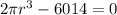
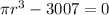
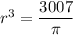
![r = \sqrt[3]{(3007)/(\pi)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/xbl91ki51hr0whwmg13glm0fzzsa0sci82.png)
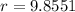
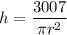
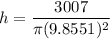
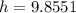
radius = 9.8551 cm
height = 9.8551 cm
b.
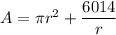
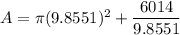
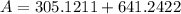
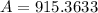
area = 915.3633 cm^2