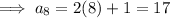Answer:
n = 17
Explanation:
Method 1
The difference between the 5th and 6th terms is 13 - 11 = 2
Therefore, the next term can be found by adding 2 each time.
If we continue with this sequence, we get:
5 = 11
6 = 13
7 = 13 + 2 = 15
8 = 15 + 2 = 17
9 = 17 + 2 = 19
10 = 19 + 2 = 21
So n = 17
-------------------------------------------------------------------------------------
Method 2
Arithmetic sequence
General form of an arithmetic sequence:
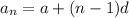
where:
 is the nth term
is the nth term- a is the first term
- d is the common difference between terms
Given terms of the sequence:
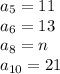
The common difference can be found by subtracting one term from the next term:
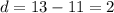
To find a, substitute the found value of d into the equation for one of the given terms:
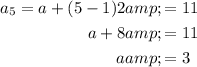
Therefore, the formula to find the nth term is:
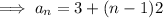

So, the 8th term is: