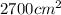Question

Maria wraps the gift she is taking to a friend’s birthday party. She doesn’t have much paper, so she does not overlap any of the edges. The dimensions of the box are: width is 30 cm, length is 15 cm, and height is 20 cm. How much paper did it take to cover the gift?

Answer 1

Total paper required to wrap the gift without any overlaps:
`2700\ cm^(2)`

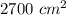
Explanation:

Here, we need to find the total paper required without any sides overlapping to wrap the gift.

The gift is of cuboid type.

Given the following:

Length = 15 cm

Width = 30 cm

Height = 20 cm

Please refer to the attached figure.

We can infer that to find the paper required, we actually need to the find the total surface area of the cuboid.

Because the gift wrap will be done on the faces of gift (which is of cuboid shape).

Formula for Surface Area of Cuboid:

`\text {Area = } 2 * (\text{Length}* \text{Width} + \text{Width}* \text{Height} + \text{Length}* \text{Height} )\\\\\Rightarrow 2 * (15 * 30 + 30 * 20 + 15 * 20)\\\Rightarrow 2 * (450 + 600 + 300)\\\Rightarrow 2 * (1350)\\\Rightarrow 2700 cm^(2)`

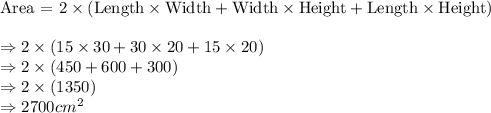
Hence, total paper required to wrap the gift without any overlaps:
`2700 cm^(2)`