Question

1. On a quiet day without many witnesses, a 4.5 ft victim is shot by a sniper that

was in a tower 780 ft away. If the angle of elevation is 48° from the victim, at
what vertical distance did the sniper shoot from?

Answer 1

The sniper shoot from 870.775 feet vertical distance.

Explanation:

Refer the attached figure

Height of victim = AB = 4.5 ft.

Distance between tower and victim BC = 780 feet

The angle of elevation =
`\angle DAE = 48^(\circ)`

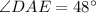
Let DE be x

AB = CE = 4.5 feet

BC =AE = 780 feet

Height of tower = DE+CE=x+4.5

In ΔDAE

`(Perpendicular)/(Base)=Tan\theta\\(DE)/(AE)=Tan 48^(\circ)\\(x)/(780)=1.11061\\x=1.11061 * 780\\x=866.275`

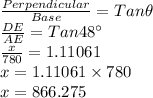
Height of tower = DE+CE=x+4.5=866.275+4.5=870.775 feet

Hence the sniper shoot from 870.775 feet vertical distance.