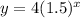Question

Find the equation of an exponential function of the form y = ab^x that passes through the points (3,13.5) and (5,30.375).

Answer 1

Let's see

• y=ab^x

Check coordinates

• 13.5=ab³-(1)

Find a

• a=13.5/b³---(2)

And

• 30.375=ab⁵

Put value from second one

• 30.375=13.5b⁵/b³
• 30.375=13.5b²
• b²=2.25
• b=1.5

Put in second one

• a=13.5/b³
• a=13.5/1.5³
• a=13.5÷3.375
• a=4

So the equation is

• y=4(1.5)^x

Answer 2

`y=4(1.5)^x`

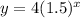
Explanation:

General form of an exponential function:
`y=ab^x`

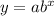
where:

• a is the y-intercept (or initial value)
• b is the base (or growth factor)
• x is the independent variable
• y is the dependent variable

If b > 1 then it is an increasing function

If 0 < b < 1 then it is a decreasing function

Given ordered pairs:

(3, 13.5) and (5, 30.375)

As the y-values are increasing, the function is increasing, so b > 1

Input the given ordered pairs into the general form of the equation:

`\implies ab^3=13.5`

`\implies ab^5=30.375`

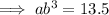
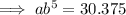
To find b, divide the second equation by the first:

`\implies (ab^5)/(ab^3)=(30.375)/(13.5)`

`\implies b^2=2.25`

`\implies b=\pm √(2.25)`

`\implies b= \pm 1.5`

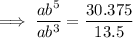
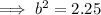
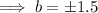
As the function is increasing, b > 1:

⇒ b = 1.5 only

Substitute the found value of b into one of the equations and solve for a:

`\implies a(1.5)^3=13.5`

`\implies 3.375a=13.5`

`\implies a=(13.5)/(3.375)`

`\implies a=4`

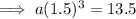
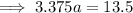
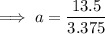
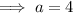
Therefore, the final exponential equation is:

`y=4(1.5)^x`