Answer:
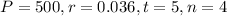
n=4 because we have a quarterly rate
After replace the values given we got:
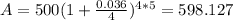
If we round this answer to the nearest number we got approximately $598 after 5 years.
Explanation:
For this case we can ue the compund interest formula for the future value given by:

Where P represent the initial amount , t the number of years and r the rate of interest on fraction. The value of n represent the number of times that the interest rate is compound in a year
For our case we have:
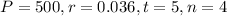
n=4 because we have a quarterly rate
After replace the values given we got:
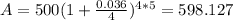
If we round this answer to the nearest number we got approximately $598 after 5 years.