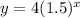Answer:
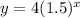
Explanation:
General form of an exponential function:
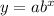
where:
- a is the y-intercept (or initial value)
- b is the base (or growth factor)
- x is the independent variable
- y is the dependent variable
If b > 1 then it is an increasing function
If 0 < b < 1 then it is a decreasing function
Given ordered pairs:
(3, 13.5) and (5, 30.375)
As the y-values are increasing, the function is increasing, so b > 1
Input the given ordered pairs into the general form of the equation:
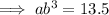
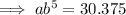
To find b, divide the second equation by the first:
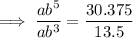
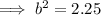
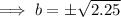
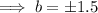
As the function is increasing, b > 1:
⇒ b = 1.5 only
Substitute the found value of b into one of the equations and solve for a:
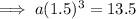
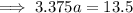
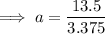
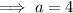
Therefore, the final exponential equation is: