Question

A manufacturing company produces steel housings for electrical equipment. The main component part of the housing is a steel trough that is made out of a 14-gauge steel coil. It is produced using a 250-ton progressive punch press with a wipedown operation that puts two 90-degree forms in the flat steel to make the trough. The distance from one side of the form to the other is critical because of weatherproofing in outdoor applications. The company requires that the width of the trough be between 8.31 inches and 8.61 inches. The widths of the troughs, in inches, collected from a sample of 49 troughs are:

8.312, 8.343, 8.317, 8.383, 8.348, 8.410, 8.351, 8.373, 8.481, 8.422, 8.476, 8.382, 8.484, 8.403, 8.414, 8.419, 8.385, 8.465, 8.498, 8.447, 8.436, 8.413, 8.489, 8.414, 8.481, 8.415, 8.479, 8.429, 8.458, 8.462, 8.460, 8.444, 8.429, 8.460, 8.412, 8.420, 8.410, 8.405, 8.323, 8.420, 8.396, 8.447, 8.405, 8.439, 8.411, 8.427, 8.420, 8.498, 8.409
a. Construct a frequency distribution and a percentage distribution.
b. Construct a cumulative percentage distribution.
c. What can you conclude about the number of troughs that will meet the company's requirements of troughs being between 8.31 and 8.61 inches wide?

Answer 1

Check the explanation

Explanation:

(a)

H0: Population mean = 8.46

H1: Population mean is not equal to 8.46

The test statistic (t) is given by the following expression -

`{t=\frac{\overline{x}-\mu_0}{s/√(n)}}`

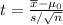
We have calculated the sample mean (8.421) and sample standard deviation (0.0461). Therefore, the test statistic (t) will be -

t = (8.421 - 8.46)/(0.0461/sqrt(49)) = -5.92

The left-sided critical value from t-distribution (two-tailed) is -2.01. Thus the test statistic falls in the rejection region and we reject the null hypothesis at 95% confidence level and conclude that the population mean is different from 8.46 inches.

(b)

There are the following four assumptions for a single sample t-test.

The observations are in ratio scale.

The observations have been taken in such a manner that every single observation is independent and uncorrelated from the others.

There should not be any significant outliers in the sample observations.

The sample data should be approximately normal.

(c)

The first assumption is true as the data is in inches. The second assumption cannot be tested now. It will depend upon the situation and study design which we assume as correct in this case. The third assumption is checked by plotting a box plot and finding the outliers. The final assumption can be checked using the Anderson-Darling normality test.

Kindly check the graphical table in the attached images below.

(d)

The data is normal (the p-value of Anderson-Darling test in > 0.05). However, two points in the Box plot are outliers though not grossly different from the entire sample data set. So, we conclude that the assumptions are valid in this case for conducting the t-test.