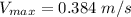Question

2) [25 pts] The bob of mass m=5 kg shown in the figure is being held by a force F. If the angle is 0⃗

θ
⃗
3) [25 pts] A cubic block of side length d is in a water container as shown in the figure. Only half of the block is immersed in water and the block is being held by a rope attached to the
onlyθ=10 and the string lengthis 0.5m,(A)calculate the tension on the string and the force. If the bob is now released, (B) how long would it take for the bob to return to its initial position? (C) At what point will the bob reach its maximum velocity? (D) What is the maximum velocity of the bob?

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

a

The tension is
`T = 48.255 \ N`

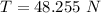
b

The time taken is
`t = 0.226 \ s`

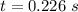
c

The position for maximum velocity is

S = 0

d

The maximum velocity is
`V_(max) =0.384 \ m/s`

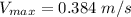
Step-by-step explanation:

The free body for this question is shown on the second uploaded image

From the question we are told that

The mass of the bob is
`m_b = 5 \ kg`

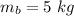
The angle is
`\theta = 10^o`

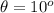
The length of the string is
`L = 0.5 \ m`

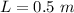
The tension on the string is mathematically represented as

`T = mg cos \theta`

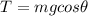
substituting values

`T = 5 * 9.8 cos(10)`

`T = 48.255 \ N`

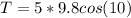
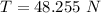
The motion of the bob is mathematically represented as

`S = A sin (w t + (\pi )/(2) )`

=>
`S = A sin (wt)`

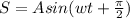
Where
`w` is the angular speed

and
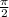`(\pi)/(2)` is the phase change

At initial position S = 0

So
`wt = cos^(-1) (0)`

`wt = 1`

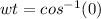
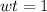
Generally
`w` can be mathematically represented as

`w = (2 \pi )/(T)`

Where T is the period of oscillation which i mathematically represented as

`T = 2 \pi \sqrt{(L)/(g) }`

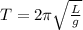
So

`t = (1)/(w)`

`t = (T)/(2 \pi)`

`t = \sqrt{(L)/(g) }`

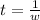
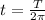
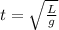
substituting values

`t = \sqrt{(0.5)/(9.8) }`

`t = 0.226 \ s`

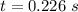
Looking at the equation

`wt = 1`

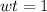
We see that maximum velocity of the bob will be at S = 0

i. e
`w = (1)/(t)`

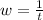
The maximum velocity is mathematically represented as

`V_(max) = w A`

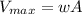
Where A is the amplitude which is mathematically represented as

`A = L sin \theta`

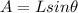
So

`V_(max) = (2 \pi )/(T ) L sin \theta`

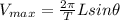
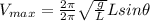`V_(max) = (2 \pi )/(2 \pi ) \sqrt{(g)/(L) } L sin \theta` Recall
`T = 2 \pi \sqrt{(L)/(g) }`

`V_(max) = √(gL) sin \theta`

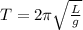
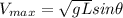
substituting values

`V_(max) = √(9.8 * 0.5 ) sin (10)`

`V_(max) =0.384 \ m/s`