Question

The volume of a cone is 3x* cubic units and its height is x units.

Which expression represents the radius of the cone's base, in units?
O 3x
6x
370x2
O 90X2
Mark this and retum
Save and Exit
Next
Submit

Answer 1

The radius of a cone is
`(3)/(√(\pi) )\ \text{units}`.

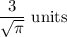Explanation:

The formula of the volume of a cone is given by :

`V=(1)/(3)\pi r^2 h`

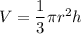
r is radius of cone

h is height of cone

We have,

Volume of a cone is 3x cubic units and height is x units. Putting the values of volume and height such that,

`r=\sqrt{(3V)/(\pi h)}\\\\r=\sqrt{(3* 3x)/(\pi x)} \\\\r=\sqrt{(3* 3)/(\pi)}\\\\r=\sqrt{(9)/(\pi)}\\\\r=(3)/(√(\pi) )\ \text{units}`

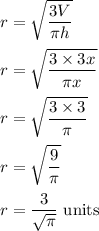
So, the radius of a cone is
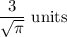`(3)/(√(\pi) )\ \text{units}`.