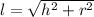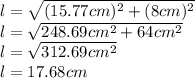Answer:
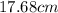
Explanation:
Using the area formula of a cone, find the height first.
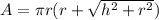
Solve for h,
Begin by dividing by
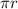

Subtract r.
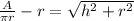
Square both sides.
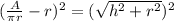
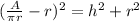
Subtract

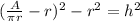
Extract the square root.
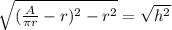
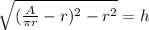
Plug in your values.
![\sqrt{[(670cm^2)/((3.14)(8cm))-(8cm)]^2-(8cm)^2 } =h](https://img.qammunity.org/2021/formulas/mathematics/high-school/wh9jjgl3s0ewj90e0kvr0mewpk7aosonuj.png)
Solve;
![\sqrt{[(670cm^2)/(25.12cm)-(8cm)]^2-(8cm)^2 } =h](https://img.qammunity.org/2021/formulas/mathematics/high-school/9kynvonghsq1nboatfv68ic824pj2w0d7b.png)
![√([26.67cm-(8cm)]^2-(8cm)^2 ) =h](https://img.qammunity.org/2021/formulas/mathematics/high-school/xypnl2l282w9lprxps5u3xcobx2p286u6y.png)
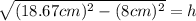

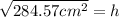
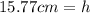
------------------------------------------------------------------
Now, to find the slant height use this formula: