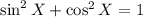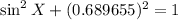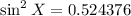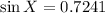Answer:
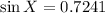
Explanation:
For angle X, 2.0 ft is the adjacent leg. 2.9 ft is the hypotenuse.
The trig ratio that relates the adjacent leg to the hypotenuse is the cosine.
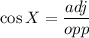

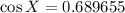
Since we now know the value of cos X, we can find the value of sin X by using the trig identity