Answer:
Domain: x ≠ -2, 3
Explanation:
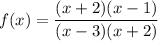
The domain (x-values) of a rational function is all real numbers of x with the exception of those for which the denominator is 0. Therefore, to find the values of x that need to be excluded from the domain, equate the denominator to zero and solve for x.
The denominator for the given function is
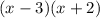

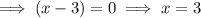
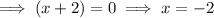
There will be a hole at x = -2 and an asymptote at x = 3.
So the values of x that need to be excluded from the domain are:
x = 3 and x = -2
Therefore, the domain of the given rational function is: x ∈ R