Question

You are wakeboarding on a river. You travel 2 miles downstream to a marina for supplies, and then you travel 3 miles upstream to a dock. The boat travels x miles per hour during the entire trip, and the river current is 3 miles per hour.

How long will the trip take when then speed of the boat is 18 miles per hour? Round to the nearest tenth minute.

Answer 1

Let x represent the speed of of boat.

We have been given that the river current is 3 miles per hour.

The speed of boat upstream will be
`x-3`.

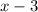The speed of boat downstream would be
`x+3`.

`\text{Time}=\frac{\text{Distance}}{\text{Speed}}`

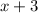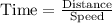
We have been given that you travel 2 miles downstream to a marina for supplies, and then you travel 3 miles upstream to a dock.

We can represent this information in an equation as:

`\text{Time}=(2)/(x+3)+(3)/(x-3)`

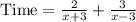
Since the speed of the boat is 18 miles per hour, so we will substitute
`x=18` in above equation and solve for time.

`\text{Time}=(2)/(18+3)+(3)/(18-3)`

`\text{Time}=(2)/(21)+(3)/(15)`

`\text{Time}=(2)/(21)+(1)/(5)`

`\text{Time}=(2\cdot 5)/(21\cdot 5)+(1\cdot 21)/(5\cdot 21)`

`\text{Time}=(10)/(105)+(21)/(105)`

`\text{Time}=(31)/(105)`

`\text{Time}=0.295238095`

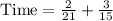
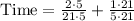
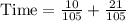
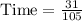
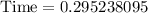
Since time is in hours, so let us convert our given time in minutes.

1 hour = 60 minutes.

`\text{Time}=0.295238095* 60\text{ minutes}`

`\text{Time}=17.7142857\text{ minutes}`

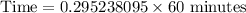
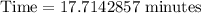
Rounding to nearest tenth of minute.

`\text{Time}\approx 17.7\text{ minutes}`

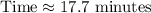
Therefore, it will take approximately 17.7 minutes for the boat to take the trip.