Answer:
is 171.8 degrees
Explanation:
Length of arc subtended by any angle
 with a radius r is given by
with a radius r is given by
 .
.
For example
to calculate length of circumference
angle subtended by whole circle is 2

Therefore length of circumference is
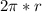
Similarly we can see that for semicircle angle at center is

hence length of arc is
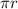
____________________________________________
Given in the problem length of arc = 3r
radius= r
let the value of angle be

Plug in the value of length of arc in formula to calculate length of arc we have
3r =

 = 3r/r = 3
= 3r/r = 3
This value of angle subtended is in radian, we need to convert radian into degrees.
_____________________________________
We know that
 is equivalent to 180 degrees.
is equivalent to 180 degrees.
Also value of
 is 3.14
is 3.14
hence 3.14 radian= 180 degrees
=>3.14/3.14 = 180/3.14 ----degrees dividing both side with 3.14
=> 1 radian = 57.325 degrees
=> 1*3 radian = 57.325 * 3 degrees( multiplying both side with 3 as we need to find value of 3 radian into degrees
=> 3 radian = 171.8 degrees.
the measurement of the angle that subtended by the arc is 171.8 degrees or in radian 3 radian