Answer:
D
Explanation:
The required line is perpendicular bi sector. So it goes through the midpoint of AB. Find the midpoint of AB
Midpoint
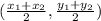
Midpoint of AB =
![((-2 + [-4])/(2) , (8+2)/(2))](https://img.qammunity.org/2021/formulas/mathematics/middle-school/5mtoq9qdprdt5et8pxoi93wno1x2lqe21j.png)
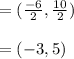
Find the slope of AB,
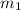
slope =
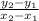
![=(2 - 8)/(-4-[-2])\\\\=(-6)/(-4+2)\\\\=(-6)/(-2)\\\\=3](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ktc8vuriq2s1m8p29uo7u1zsjzpcoqsw0k.png)
Slope of the perpendicular line to AB =
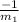 = -1/3
= -1/3
The required line passes through (-3, 5) and has slope -1/3
Equation of required line : y - y1 = m (x -x1)
![y - 5 = (-1)/(3) (x - [-3])\\\\y-5=(-1)/(3) ( x +3)\\\\y-5=(-1)/(3)x + 3 *(-1)/(3)\\\\y-5=(-1)/(3)x-1\\\\y=(-1)/(3)x-1+5\\\\y=(-1)/(3)x + 4](https://img.qammunity.org/2021/formulas/mathematics/middle-school/9bnzk0lsxpl1h7x30jvgqldj5i24ho5rxi.png)