Question

In the diagram below, \overrightarrow{QR}

QR
​
Q, R, with, \overrightarrow, on top is perpendicular to \overline{BD}
BD
start overline, B, D, end overline.

Find the length of \overline{BD}
BD
start overline, B, D, end overline.

Answer 1

24 units

Explanation:

Answer 2

We have been given a diagram of two similar triangles. We are asked to find the measure of segment BD.

We can see that segment AB and CD are perpendicular to segment BD as they form right angle with BD.

We have been given that segment QR is perpendicular to BD, so segment AB, CD and QR are parallel.

Using parallel lines properties, we can see that angle BAQ is equal to DCQ and angle AQB is equal to angle CQD and both angles have a right triangle.

So both triangles are similar. We know that corresponding sides of similar triangles are proportional.

`(QD)/(CD)=(BQ)/(AB)`

`(QD)/(19.2)=(15)/(32)`

`(QD)/(19.2)\cdot 19.2=(15)/(32)\cdot 19.2`

`QD=9`

`BD=BQ+QD`

`BD=15+9`

`BD=24`

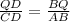
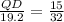
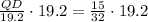
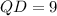
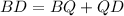
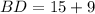
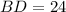
Therefore, the length of segment BD will be 24 units.