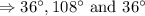Answer:
Explanation:
In
 , sides AB = AC.
, sides AB = AC.
We know the property that angles opposite to equal sides in a triangle are equal.
Hence,
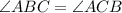
Let this angle be x.
So,

Similarly, in
Hence,
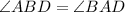
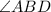 and
and
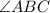 are same.
are same.
By equation (1):
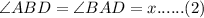
Similarly, in
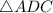 :
:
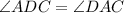
Let this angle be y.

We know that sum of all three angles in a triangle is equal to
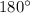 .
.
In
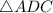 , sum of all three angles:
, sum of all three angles:
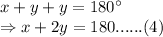
In
 , sum of all three angles:
, sum of all three angles:
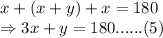
Using elimination method to solve equation (4) and (5):
Multiplying equation (5) by 2 and subtracting (4) from it:
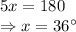
Putting value of x in (4):
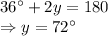
So, angles of
 are:
are:
x, (x+y) and y