Answer:
1. Volume of the composite figure is 943.89 mm³
2. The volume, of the is 144 cm³
Explanation:
1. The composite figure comprises of a cube and a half cylinder;
Volume of a cube = 9 mm × 11 mm × 6 mm = 594 mm³
Volume of the half cylinder = area of base × length = (π·r²)/2 × l
Where:
r = (Diameter of base)/2 = 9/2 = 4.5 mm
l = 11 mm
Therefore, plugging the values, gives;
Volume of the half cylinder = (π × 4.5²)/2 × 11 = 349.89 mm³
Hence, volume of the composite figure = Volume of the cube + Volume of the half cylinder
Volume of the composite figure = 594 mm³ + 349.89 mm³ = 943.89 mm³
2. The volume, V of a pyramid is given by the following relation;

Where:
l = Length of base = 8 cm
w = Width of the base = 6 cm
h = Height of the pyramid = 9 cm
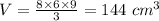
Here we have that a cube of side x, therefore, the area = x·x, integrating we have;
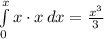
Where:
Length, height width of the pyramid = x
It can therefore be shown, that for a pyramid of length, l, width, w, and height, h, the volume,
 .
.