Answer:
The rabbit population will reach its peak after 10 years.
Explanation:
Suppose we have a quadratic function in the following format:
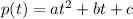
The vertex of the function is the point:
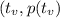
In which
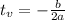
If a is negative, the vertex is a peak.
In this question:
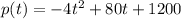
So
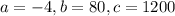
According to this quadratic function, after how many years will the rabbit population reach its peak
This is
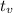
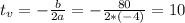
The rabbit population will reach its peak after 10 years.