Question

From a number of apples a man sells half number existing apples plus 1 to first customer,sells 1/3rd of the remaining apples plus 1 to second customer and 1/5th of the remaining apples plus 1 to third customer. He finds that he has 3 apples remaining. How many apples he originally had

Answer 1

20 apples

Explanation:

Let the number of apples = x

First customer:

Sold apples = (1/2) of x + 1

`=(x)/(2)+1\\`

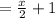
Remaining apples

`=x -((x)/(2)+1)\\\\=x - (x)/(2)-1\\\\=(x)/(2)-1\\`

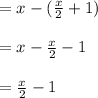
Second customer:

Sold apples = (1/3) of remaining apples + 1

`=(1)/(3)*((x)/(2)-1)+1\\\\=[(1)/(3)*(x)/(2)]- (1)/(3)*1+1\\\\=(x)/(6)-(1)/(3)+1\\\\=(x)/(6)-(1)/(3)+(3)/(3)\\\\=(x)/(6)+(2)/(3)\\`

Remaining apples =

`=((x)/(2)-1)-((x)/(6)+(2)/(3))\\\\=(x)/(2)-1-(x)/(6)-(2)/(3)\\\\=(x)/(2)-(x)/(6)-1-(2)/(3)\\\\=(3x)/(6)-(x)/(6)-(3)/(3)-(2)/(3)\\\\=(2x)/(6)-(5)/(3)\\\\=(x)/(3)-(5)/(3)`

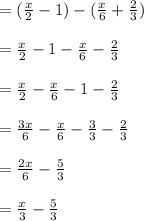
Third customer:

Sold apples = (1/5) of reaming apples +1

`=(1)/(5)*[(x)/(3)-(5)/(3)]+1\\\\=(1)/(5)*(x)/(3)-(1)/(5)*(5)/(3)+1\\\\=(x)/(15)-(1)/(3)+1\\\\=(x)/(15)-(1)/(3)+(3)/(3)\\\\=(x)/(15)+(2)/(3)\\\\`

Remaining apples =

`=(x)/(3)-(5)/(3)-[(x)/(15)+(2)/(3)]\\\\=(x)/(3)-(5)/(3)-(x)/(15)-(2)/(3)\\\\=(x)/(3)-(x)/(15)-(5)/(3)-(2)/(3)\\\\=(5x)/(15)-(x)/(15)-(7)/(3)\\\\=(4x)/(15)-(7)/(3)\\`

Remaining apples with the man = 3

`(4x)/(15)-(7)/(3)=3\\\\(4x)/(15)=3+(7)/(3)\\\\(4x)/(15)=(9)/(3)+(7)/(3)\\\\(4x)/(15)=(16)/(3)\\\\x=(16)/(3)*(15)/(4)\\\\x=4*5`

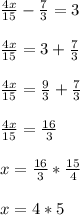
x = 20

He had 20 apples