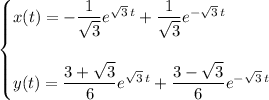Question

X' + 2y' + x = 0 , x' - y' + y = 0 x(0) = 0 and y(0) = 1

Answer 1

This looks like a system of differential equations.

`\begin{cases}x' + 2y' + x = 0 \\ x' - y' + y = 0 \\x(0)=0, y(0)=1\end{cases}`

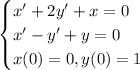
Eliminating x' gives

`(x'+2y'+x)-(x'-y'+y) = 0 - 0 \implies 3y' - y + x = 0`

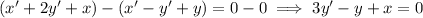
and eliminating y' gives

`(x'+2y'+x) + 2(x'-y'+y)=0+2*0 \implies 3x' + x + 2y = 0`

so that we can rewrite the system as

`\begin{cases}3x' = -x - 2y \\ 3y' = -x + y\end{cases}`

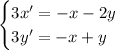
or equivalently in matrix form as

`\begin{bmatrix}x\\y\end{bmatrix}' = \frac13 \begin{bmatrix}-1&-2\\-1&1\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}`

Compute the eigenvalues for the coefficient matrix:

`\det\begin{bmatrix}-1-\lambda&-2\\-1&1-\lambda\end{bmatrix} = (-1-\lambda)(1-\lambda) - 2 = \lambda^2 -3 = 0 \implies \lambda=\pm\sqrt3`

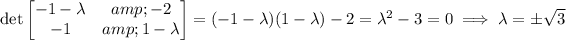
Compute the corresponding eigenvectors:

`\lambda=\sqrt3 \implies \begin{bmatrix}-1-\sqrt3&-2\\-1&1-\sqrt3\end{bmatrix}\begin{bmatrix}v_1\\v_2\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix} \\\\ \implies v_1=(1-\sqrt3)v_2 \implies \vec v = \begin{bmatrix}1-\sqrt3\\1\end{bmatrix}`

`\lambda=-\sqrt3 \implies \begin{bmatrix}-1+\sqrt3&-2\\-1&1+\sqrt3\end{bmatrix}\begin{bmatrix}v_1\\v_2\end{bmatrix}=\begin{bmatrix}0\\0\end{bmatrix} \\\\ \implies v_1 = (1+\sqrt3)v_2 \implies \vec v = \begin{bmatrix}1+\sqrt3\\1\end{bmatrix}`

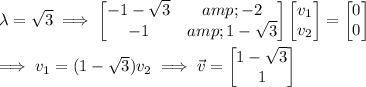
We end up multiplying the matrix by 1/3, so the eigenvalues also get scaled by 1/3 and λ = ±1/√3. The eigenvectors stay the same.

Then the characteristic solution to the system is

`\begin{bmatrix}x\\y\end{bmatrix} = C_1 e^(t/\sqrt3) \begin{bmatrix}\frac{1-\sqrt3}3\\\frac13\end{bmatrix} + C_2 e^(-t/\sqrt3) \begin{bmatrix}\frac{1+\sqrt3}3\\\frac13\end{bmatrix}`

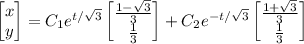
Use the initial conditions to solve for the constants.

`\begin{bmatrix}0\\1\end{bmatrix} = C_1 \begin{bmatrix}\frac{1-\sqrt3}3\\\frac13\end{bmatrix} + C_2 \begin{bmatrix}\frac{1+\sqrt3}3\\\frac13\end{bmatrix}`

`\implies \begin{cases}(1-\sqrt3) C_1 + (1+\sqrt3) C_2 = 0 \\ C_1 + C_2 = 3\end{cases}`

`\implies C_1=\frac{3+\sqrt3}2, C_2=\frac{3-\sqrt3}2`

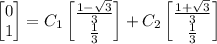
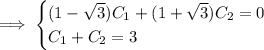
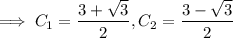
Then the particular solution is

`\begin{bmatrix}x\\y\end{bmatrix} = \frac{3+\sqrt3}6 e^(t/\sqrt3) \begin{bmatrix}1-\sqrt3\\1\end{bmatrix} + \frac{3-\sqrt3}6 e^(-t/\sqrt3) \begin{bmatrix}1+\sqrt3\\1\end{bmatrix}`

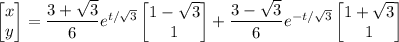
or

`\begin{cases}x(t) = -\frac1{\sqrt3} e^(\sqrt3 \, t) + \frac1{\sqrt3} e^(-\sqrt3\,t) \\\\ y(t) = \frac{3+\sqrt3}6 e^(\sqrt3\,t) + \frac{3-\sqrt3}6 e^(-\sqrt3\,t)\end{cases}`