Question

Hershel is designing a square pyramid that needs to have a lateral surface of 440 in². The area of the base is 121 in². Find the length of the slant height of the pyramid.

Answer 1

The length of the slant height of the square pyramid is 20 in.

Explanation:

The lateral surface area of a regular pyramid is the sum of the areas of its lateral faces.

The general formula for the lateral surface area of a regular pyramid is

`A=(1)/(2)pl`

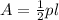
where
`p` represents the perimeter of the base and
`l` the slant height.

From the information given we know that:

• The lateral surface area of a square pyramid is 440 in².
• The area of the base is 121 in².

And we want to find the the slant height of the pyramid.

For this, we also need to know that the area of a square is given by
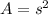`A=s^2`, where s is the length of any side and the perimeter of a square is given by
`p=4s`.

Applying the formula for the area of a square we can find the length of the side

`121=s^2\\s^2=121\\s=√(121)=11`

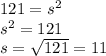
The perimeter of the base is

`p=4\cdot(11)=44`

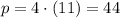
Next, we can apply the formula for the lateral surface area and solve for
`l` the slant height.

`440=(1)/(2)44l\\\\(1)/(2)\cdot \:44l=440\\\\22l=440\\\\l=20`

The length of the slant height of the square pyramid is 20 in.