Question

Which expression is equivalent to the following complex fraction?

(SEE PICTURE / TROLL ANSWERS WILL BE REPORTED / e d g e n u i t y 2020)


`-(2)/(x) + (5)/(y)` /
`(3)/(y) -(2)/(x)`
(I THINK IT MIGHT BE THE 1st or 2nd option

Answer 1

A. -2y+5x/3x-2y

Explanation:

Given the complex fraction;

`-(2)/(x) +(5)/(y) / (3)/(y) - (2)/(x) \\`

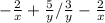
First we will find the LCM of the numerator and the denominator as shown below;

`(-2y+5x)/(xy) /(3x-2y)/(xy)`

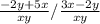
Then we divide both equation by multiplying the numerator by the reciprocal of the denominator as shown;

`= (-2y+5x)/(xy) * (xy)/(3x-2y) \\= (-2y+5x)/(3x-2y) \\`

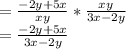
This gives the required answer